Círculos de Confusión
by , 12/04/11 at 20:22:41 (7434 Visitas)
Esta entrada en mi blog se lo dedico a Sarmale y a mi promesa de hacerle entender el concepto de círculo de confusión tal como yo lo aprendí cuando las cámaras llevaban carrete y que actualmente, con los sensores digitales, sigue funcionando igual.
En primer lugar, fijémonos en la siguiente imagen:
En esta imagen podemos apreciar como cualquier punto de la naturaleza en tres dimensiones se representa en nuestro sensor de dos dimensiones. Cualquier punto de la naturaleza refleja la luz que incide sobre el, y entra en nuestro objetivo formando un cono. Las lentes que se encuentran en el objetivo tienen como misión (explicado de una forma un tanto burda) redirigir ese cono ce luz y reagruparlo de nuevo en un solo punto, al modo de una lente cóncava:
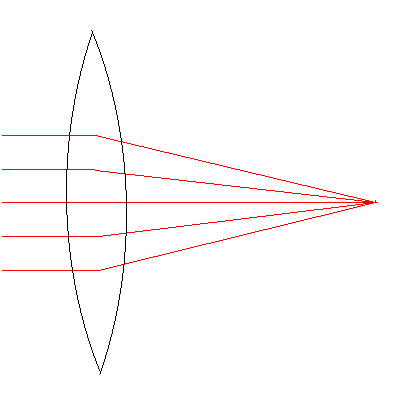
Si continuamos analizando la primera imagen, en el primer caso cualquier punto que se encuentre en el plano que estamos enfocando se representará en nuestro sensor como un punto. Es decir, su representación será real, y los infinitos puntos que se encuentren en el plano enfocado se representarán en nuestro sensor tal como son, como puntos, dibujando la imagen tal y como lo vemos.
En el segundo caso, un punto situado entre nosotros y el plano enfocado se representará por detrás de nuestro sensor. El cono de luz que forma el punto se representará por detrás del sensor, por lo que sobre él quedará impreso un círculo, resultante del corte que hace el sensor sobre dicho cono de luz.
En el tercer caso, en el punto que se encuentra por detrás del plano enfocado (más alejado de nuestra cámara), el cono de luz se representará por delante del sensor, invirtiéndose y formando de nuevo el cono que se impresionará en nuestro sensor de nuevo formando otro círculo.
En definitivas cuantas, cualquier punto que se encuentra en nuestro plano de enfoque se representará en nuestro sensor como el punto que es, mientras que cualquier punto que se encuentre por delante o por detrás de nuestro plano de enfoque se representará en el sensor como un círculo.
A estos círculos se les denomina CIRCULOS DE CONFUSIÓN.
Entonces, ¿de dónde sale la profundidad de campo?, ¿cómo es posible que veamos enfocado no solo un plano, sino que por delante y por detrás también existan puntos que se encuentran enfocados?
La respuesta es muy sencilla. Nuestro visión tiene sus limitaciones y se estima que el ojo humano ve cualquier círculo de 0.2 mm como si fuera un punto. Esto quiere decir que todos los puntos que se encuentren por delante y por detrás de nuestro plano enfocado que generen en nuestro sensor un círculo de confusión inferior a 0.2mm (esto es una aproximación) lo apreciaremos como un punto, por lo que nos provocará la sensación de que se encuentra enfocado.
¿Cuál sería entonces el motivo por el cual un sensor APSC genera menor profundidad de campo que una Full Frame?
Pongamos un ejemplo, nos ponemos a 10 metros de lo que queremos enfocar, usamos un 80mm a f5.6 y metemos estos datos en una calculadora de pdc (profundidad de campo):
Si usamos una 50D (ASPC) nos da como resultado 3,39 m de pdc
Si usamos una 5D (Full Frame) nos da como resultado 5,59 m de pdc
Otro ejemplo, a 100 metros con un 300mm a f8
La 50D nos da 34,66 m de pdc
La 5D nos da 57,22 m de pdc
Y el último ejemplo, a 20cm con un 80mm a f10
La 50D nos da 0,14 cm de pdc
La 5D nos da 0,23 cm de pdc
Fijaos en las relaciones:
5,59/3,39=1,65
57,22/34,66=1,65
0,23/0,14=1,64
¿Qué podemos deducir de estos resultados? ¿No se parecen mucho estas relaciones a nuestro factor de recorte en las canon?
Efectivamente, ese es el motivo. Los círculos de confusión se impresionan en el plano del sensor con exactamente el mismo tamaño, pero un sensor APSC lo ampliará un 60% aproximadamente más que una Full Frame cuando lo veamos en pantalla o en papel.
Aquí lo dejo. El tema da para mucho más, como el porqué la pdc es mayor por detrás que por delante el plano enfocado y porqué influyen para la pdc la distancia al plano enfocado, la abertura del diafragma o la focal utilizada. Pero eso ya es motivo para otro capítulo...










